სფერო (Sphere)
1. რა არის სფერო?
გეომეტრიაში სფერო არის სამგანზომილებიანი (3D) მრგვალი ფორმის სხეული. სხვა სამგანზომილებიანი ფიგურებისგან (მაგალითად, კუბისგან ან პირამიდისგან) განსხვავებით, სფეროს არ გააჩნია არც წვეროები და არც წიბოები.
მათემატიკური განმარტება: სფერო არის სივრცეში იმ წერტილთა სიმრავლე, რომლებიც თანაბარი მანძილითაა დაშორებული ერთი კონკრეტული წერტილიდან — ცენტრიდან.
რეალური მაგალითები: ჩვენს გარშემო უამრავი სფერული ობიექტია: კალათბურთის ბურთი, საპნის ბუშტი, ჩოგბურთის ბურთი და სხვა. შენიშვნა: ჩვენი პლანეტა, დედამიწა, არ არის იდეალური სფერო; მას სფეროიდი ეწოდება, რადგან პოლუსებთან ოდნავ შეზნექილია, თუმცა ძალიან ჰგავს სფეროს.
2. სფეროს ძირითადი ელემენტები
სფეროს სრულყოფილად გასაგებად აუცილებელია მისი შემადგენელი ნაწილების ცოდნა:
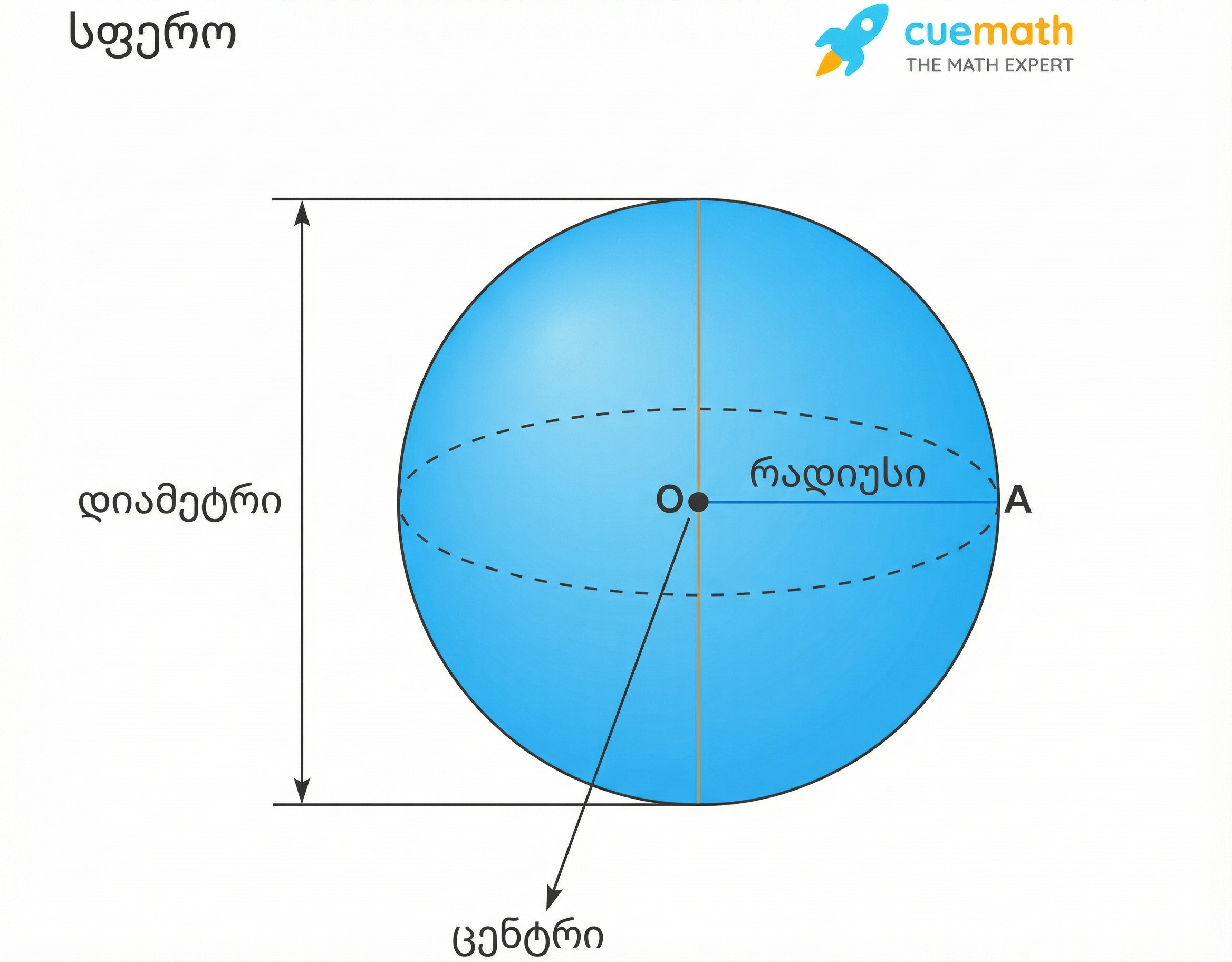
- რადიუსი (r): მონაკვეთი, რომელიც აერთებს სფეროს ცენტრს ზედაპირზე მდებარე ნებისმიერ წერტილთან. ყველა რადიუსი ერთი და იმავე სფეროსთვის ტოლია.
- დიამეტრი (d): მონაკვეთი, რომელიც გადის სფეროს ცენტრზე და აერთებს ზედაპირის ორ მოპირდაპირე წერტილს. დიამეტრი რადიუსზე ორჯერ დიდია (\(d=2r\)).
- წრეწირის სიგრძე (Circumference): სფეროს "დიდი წრეწირის" სიგრძე. ეს არის ყველაზე დიდი წრეწირი, რომელიც შეიძლება სფეროს შიგნით გაივლოს (შეიცავს ცენტრს).
- მოცულობა (V): სივრცის ის ნაწილი, რომელსაც სფერო იკავებს.
- ზედაპირის ფართობი (S): სფეროს გარე გარსის მთლიანი ფართობი.
3. ძირითადი ფორმულები
ქვემოთ მოცემულია სფეროსთან დაკავშირებული უმთავრესი მათემატიკური ფორმულები. ჩავთვალოთ, რომ სფეროს რადიუსია \(r\).
| პარამეტრი | ფორმულა | განმარტება |
|---|---|---|
| დიამეტრი | $$d = 2r$$ | რადიუსის გაორმაგებული მნიშვნელობა. |
| წრეწირის სიგრძე | $$C = 2\pi r$$ | დიდი წრეწირის სიგრძე. |
| ზედაპირის ფართობი | $$S = 4\pi r^2$$ | სრული ზედაპირის ფართობი. |
| მოცულობა | $$V = \frac{4}{3}\pi r^3$$ | სფეროს მიერ დაკავებული სივრცე. |
4. პრაქტიკული მაგალითები
ცოდნის გასამყარებლად განვიხილოთ მარტივი ამოცანები:
მაგალითი 1: დიამეტრისა და წრეწირის სიგრძის პოვნა
ამოცანა: იპოვეთ სფეროს დიამეტრი და დიდი წრეწირის სიგრძე, თუ რადიუსი 7 ერთეულია.
ამოხსნა:
მოცემულია რადიუსი \(r = 7\).
დიამეტრი \(d = 2 \times r = 2 \times 7 = 14\) ერთეული.
წრეწირის სიგრძე \(C = 2\pi r \approx 2 \times \frac{22}{7} \times 7 = 44\) ერთეული.
პასუხი: დიამეტრი არის 14, ხოლო წრეწირის სიგრძე — 44 ერთეული.
მაგალითი 2: მოცულობის პოვნა
ამოცანა: იპოვეთ სფეროს მოცულობა, თუ მისი რადიუსი 8 ერთეულია.
ამოხსნა:
მოცულობის ფორმულაა \(V = \frac{4}{3}\pi r^3\). ჩავსვათ მნიშვნელობები (\(\pi \approx \frac{22}{7}\)):
$$V = \frac{4}{3} \times \frac{22}{7} \times 8^3$$
$$V = \frac{4}{3} \times \frac{22}{7} \times 512 \approx 2145.52 \text{ კუბური ერთეული}$$
პასუხი: სფეროს მოცულობაა 2145.52 კუბური ერთეული.
მაგალითი 3: ზედაპირის ფართობის პოვნა
ამოცანა: იპოვეთ სფეროს ზედაპირის ფართობი, თუ რადიუსი 5 ერთეულია.
ამოხსნა:
ზედაპირის ფართობის ფორმულაა \(S = 4\pi r^2\). ჩავსვათ მნიშვნელობები:
$$S = 4 \times \frac{22}{7} \times 5^2$$
$$S = 4 \times \frac{22}{7} \times 25 \approx 314.28 \text{ კვადრატული ერთეული}$$
პასუხი: სფეროს ზედაპირის ფართობია 314.28 კვადრატული ერთეული.