კვადრატი (Square)
1. რა არის კვადრატი?
გეომეტრიაში კვადრატი არის ერთ-ერთი ყველაზე ფუნდამენტური და სიმეტრიული ფიგურა. ის წარმოადგენს ოთხკუთხედს, რომელსაც აქვს ოთხი ტოლი გვერდი და ოთხი მართი კუთხე. ჩვენს გარშემო უამრავი საგანია კვადრატული ფორმის — ჭადრაკის დაფიდან დაწყებული, კედლის საათით დამთავრებული.
განმარტების თანახმად, კვადრატი არის დახურული, ორგანზომილებიანი (2D) ფიგურა ოთხი გვერდით. მისი უნიკალურობა იმაში მდგომარეობს, რომ ოთხივე გვერდი ერთმანეთის ტოლია და პარალელური.
კვადრატის ძირითადი მახასიათებლები:
- მოპირდაპირე გვერდები პარალელურია.
- ყველა გვერდი სიგრძით ტოლია.
- ყველა კუთხე არის \(90^\circ\).
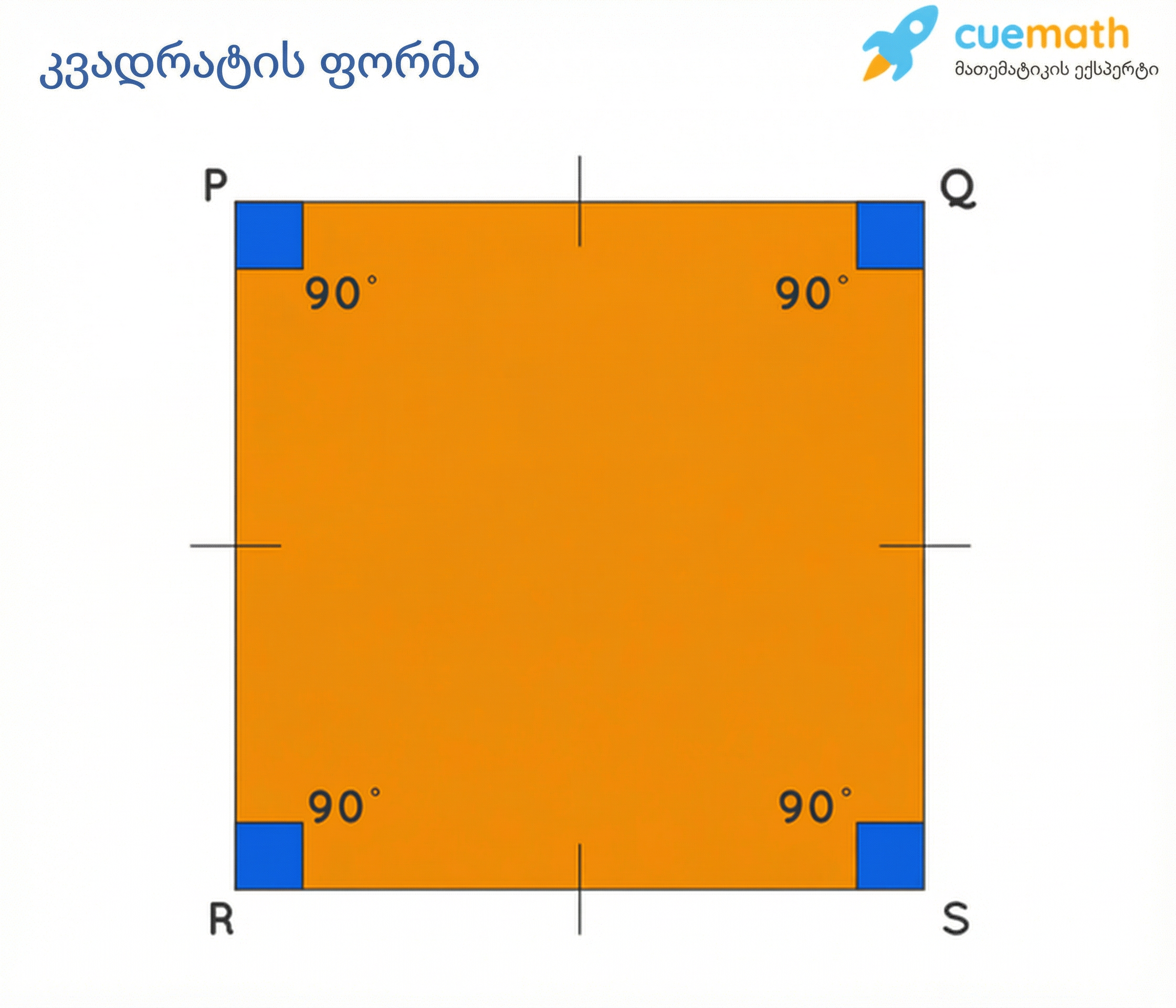
2. კვადრატის თვისებები
როგორც მათემატიკოსი, გირჩევთ, ყურადღება მიაქციოთ კვადრატის თვისებებს, რადგან ისინი გვეხმარება რთული ამოცანების მარტივად გადაჭრაში:
- გვერდები და წვეროები: კვადრატს აქვს 4 გვერდი და 4 წვერო.
- კუთხეები: თითოეული შიდა კუთხე \(90^\circ\)-ია. შესაბამისად, შიდა კუთხეების ჯამი \(360^\circ\)-ია.
- პარალელურობა: მოპირდაპირე გვერდები ერთმანეთის პარალელურია (ამიტომ კვადრატი ასევე არის პარალელოგრამი).
- დიაგონალები:
- დიაგონალების სიგრძე ტოლია.
- ისინი ერთმანეთს კვეთენ და შუაზე ყოფენ \(90^\circ\)-იანი კუთხით.
- დიაგონალი კვადრატს ყოფს ორ ტოლ (კონგრუენტულ) სამკუთხედად.
- დიაგონალის სიგრძე ყოველთვის მეტია კვადრატის გვერდის სიგრძეზე.
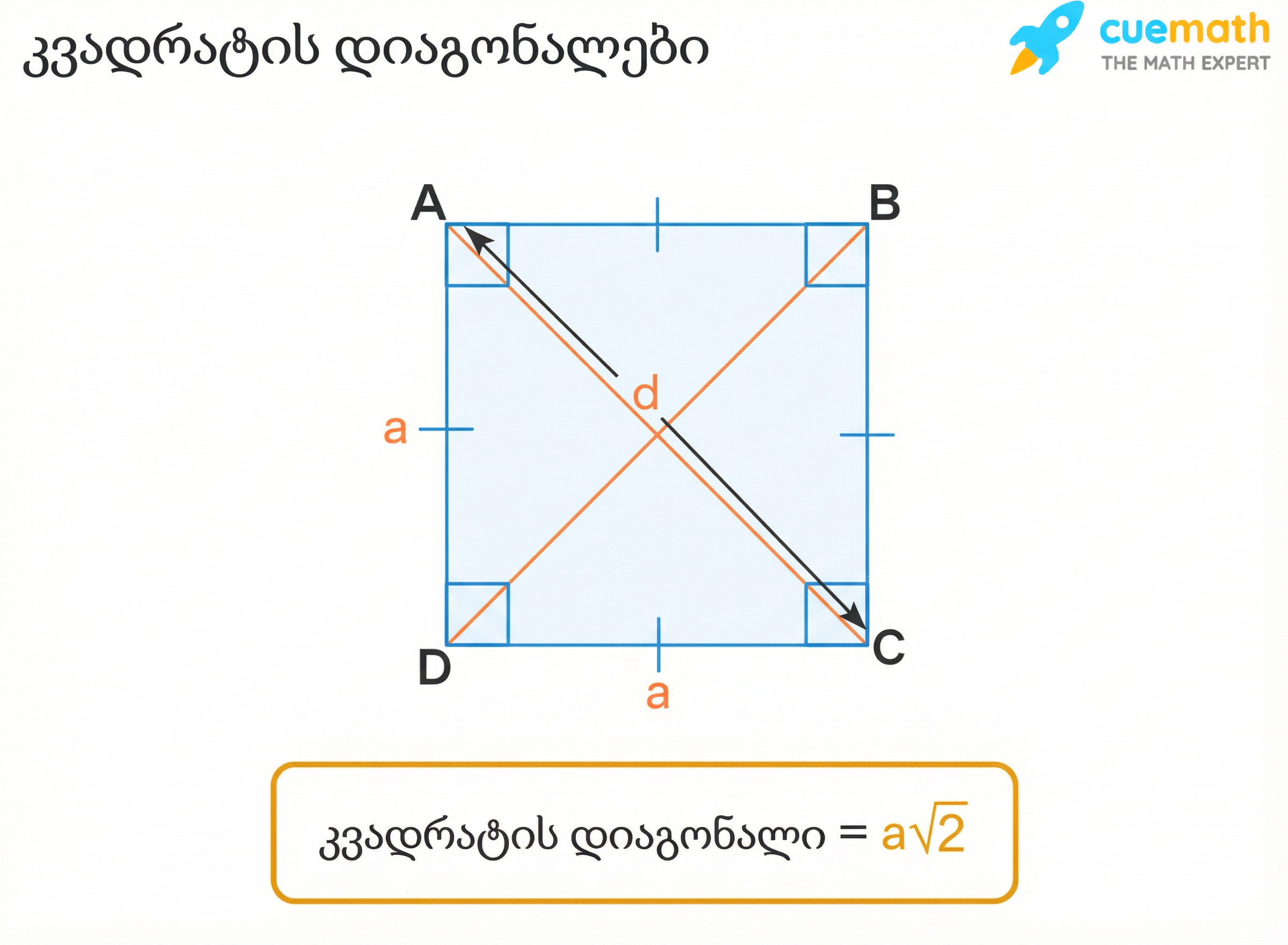
კვადრატი თუ მართკუთხედი?
ხშირად ისმის კითხვა: რა საერთო აქვთ მათ? ორივე ფიგურას აქვს 4 გვერდი, 4 წვერო, პარალელური მოპირდაპირე გვერდები და \(90^\circ\)-იანი კუთხეები. მთავარი განსხვავება ისაა, რომ კვადრატში აუცილებელია ყველა გვერდი ტოლი იყოს, ხოლო მართკუთხედში მხოლოდ მოპირდაპირე გვერდებია ტოლი.
დაიმახსოვრეთ: ყველა კვადრატი მართკუთხედია, მაგრამ ყველა მართკუთხედი არ არის კვადრატი.
3. კვადრატის ფორმულები
პრაქტიკული გამოთვლებისთვის ვიყენებთ სამ ძირითად ფორმულას. დავუშვათ, კვადრატის გვერდის სიგრძე არის \(a\).
ა) ფართობი (\(S\))
ფართობი არის სივრცე, რომელსაც იკავებს ფიგურა. იზომება კვადრატულ ერთეულებში (მაგ: სმ², მ²).
ბ) პერიმეტრი (\(P\))
პერიმეტრი არის საზღვრების საერთო სიგრძე. რადგან ოთხივე გვერდი ტოლია, იზომება წრფივ ერთეულებში (მაგ: სმ, მ).
გ) დიაგონალი (\(d\))
დიაგონალი აერთებს ორ არამეზობელ წვეროს. პითაგორას თეორემის გამოყენებით (\(d^2 = a^2 + a^2\)), ვიღებთ:
4. კვადრატის აგება (ნაბიჯ-ნაბიჯ)
კვადრატის ზუსტი აგებისთვის დაგჭირდებათ სახაზავი და ფარგალი. განვიხილოთ მაგალითი, სადაც გვერდის სიგრძე 6 სმ-ია.
- მონაკვეთის გავლება: სახაზავით გაავლეთ 6 სმ სიგრძის PQ მონაკვეთი.
- პერპენდიკულარის მომზადება: გააგრძელეთ PQ ხაზი მარჯვნივ. დაადეთ ფარგალი Q წერტილს და გააკეთეთ აღნიშვნები (რკალები) Q-ს ორივე მხარეს (დავარქვათ U და V).
- პერპენდიკულარის აგება: დაადეთ ფარგალი U და V წერტილებს და გაავლეთ რკალები Q-ს ზემოთ ისე, რომ ერთმანეთი გადაკვეთონ. გადაკვეთის წერტილს დაარქვით W. შეაერთეთ Q და W. ეს არის მართი კუთხე (\(90^\circ\)).
- გვერდის მონიშვნა: ფარგალი გაშალეთ ზუსტად 6 სმ-ზე. დაადეთ Q წერტილს და გააკეთეთ აღნიშვნა QW ხაზზე. ამ წერტილს დაარქვით R.
- ბოლო წვეროს პოვნა:
- ფარგალი კვლავ 6 სმ-ზე დატოვეთ.
- დაადეთ P წერტილს და გაავლეთ რკალი ზემოთ.
- დაადეთ R წერტილს და გაავლეთ რკალი ისე, რომ გადაკვეთოს წინა რკალი.
- გადაკვეთის წერტილი არის S.
- შეერთება: შეაერთეთ წერტილები P, Q, R, S. თქვენ მიიღეთ იდეალური კვადრატი.
5. პრაქტიკული მაგალითები
ცოდნის გასამყარებლად განვიხილოთ მარტივი ამოცანები:
ამოცანა 1: ფართობის პოვნა
ამოცანა: თუ კვადრატის გვერდი 5 სმ-ია, რას უდრის ფართობი?
ამოხსნა:
$$S = 5^2 = 25 \text{ სმ}^2$$
ამოცანა 2: დიაგონალის პოვნა
ამოცანა: იპოვეთ კვადრატის დიაგონალი, თუ გვერდი 4 სმ-ია.
ამოხსნა:
$$d = 4\sqrt{2} \approx 5.66 \text{ სმ}$$