კონუსი (Cone)
1. რა არის კონუსი? (ძირითადი ელემენტები)
მოგესალმებით კონუსის სამყაროში. გეომეტრიაში კონუსი არის სამგანზომილებიანი (3D) ფიგურა, რომელსაც აქვს წრიული ფუძე და ერთი წვერო. ის ვიწროვდება ფუძიდან წვერომდე. საუკეთესო ვიზუალური მაგალითია ნაყინის "ჭიქა" ან სადღესასწაულო ქუდი.
ამ გვერდზე თქვენ შეისწავლით კონუსის ელემენტებს, ფორმულებსა და პრაქტიკულ მაგალითებს.
კონუსის შემადგენელი ნაწილები:
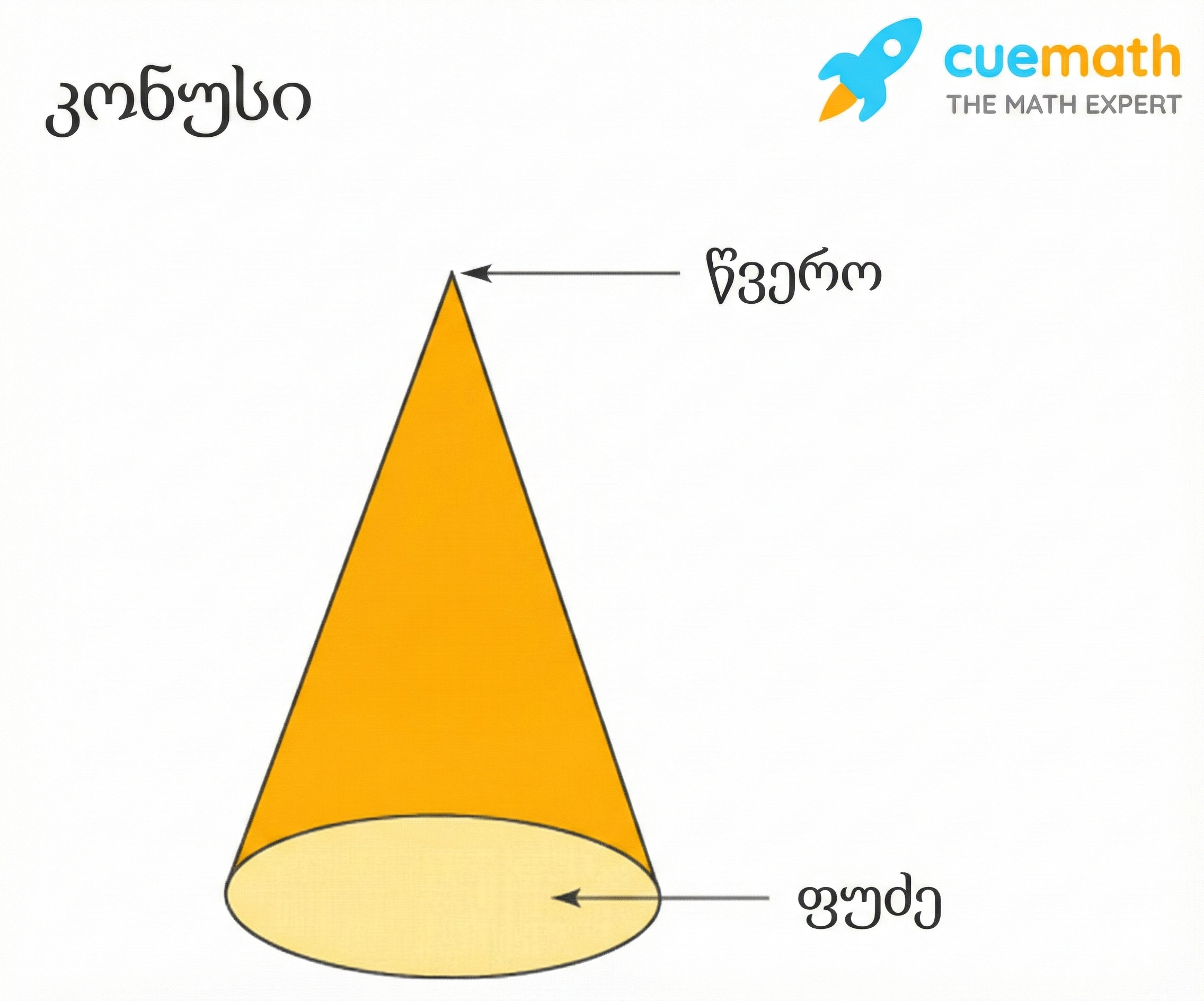
- ფუძე (Base): ბრტყელი ზედაპირი, რომელიც წრეს წარმოადგენს.
- წვერო (Vertex / Apex): წერტილი, სადაც კონუსის გვერდითი ზედაპირი იყრის თავს (ფუძის მოპირდაპირედ).
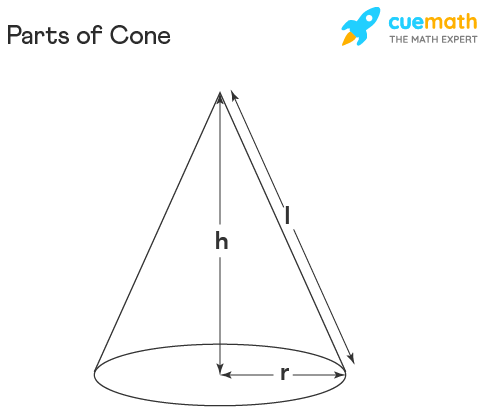
- რადიუსი (\(r\)): მანძილი ფუძის (წრის) ცენტრიდან მის კიდემდე.
- სიმაღლე (\(h\)): მართობი, დაშვებული წვეროდან ფუძის ცენტრამდე.
- მსახველი (\(l\) - Slant Height): მანძილი წვეროდან ფუძის წრეწირის ნებისმიერ წერტილამდე.
2. კონუსის ტიპები
არსებობს ძირითადად ორი ტიპის კონუსი:
მართი კონუსი (Right Circular Cone)
როდესაც კონუსის წვერო ზუსტად ფუძის ცენტრის თავზეა. ამ შემთხვევაში, სიმაღლე ფუძის მართობულია.
დახრილი კონუსი (Oblique Cone)
როდესაც წვერო არ მდებარეობს ფუძის ცენტრის გასწვრივ, არამედ გადახრილია გვერდზე.
ჩვენი გზამკვლევი ძირითადად ფოკუსირებულია მართ კონუსზე, რადგან სასკოლო და საუნივერსიტეტო გეომეტრიაში ის ყველაზე ხშირად გამოიყენება.
3. კონუსის ფორმულები
ეს არის ყველაზე მნიშვნელოვანი ნაწილი ნებისმიერი მათემატიკური ამოცანის გადასაჭრელად.
ა) მსახველის პოვნა (\(l\))
მართ კონუსში რადიუსი, სიმაღლე და მსახველი ქმნიან მართკუთხა სამკუთხედს. პითაგორას თეორემის მიხედვით:
ბ) კონუსის მოცულობა (\(V\))
კონუსის მოცულობა ტოლია იმავე ფუძისა და სიმაღლის მქონე ცილინდრის მოცულობის ერთი მესამედის.
\(\pi \approx 3.14\)
გ) ზედაპირის ფართობი (\(S\))
ზედაპირის ფართობი იყოფა ორ ნაწილად: გვერდითი ზედაპირი და სრული ზედაპირი.
გვერდითი ზედაპირის ფართობი (LSA): მხოლოდ დახრილი ნაწილი, ფუძის გარეშე.
სრული ზედაპირის ფართობი (TSA): გვერდით ზედაპირს პლუს ფუძის (წრის) ფართობი.
4. შედარებითი ცხრილი: კონუსის თვისებები
| თვისება | აღწერა |
|---|---|
| წახნაგების რაოდენობა | 1 (თუ ფუძეს არ ჩავთვლით) ან 2 (ფუძესთან ერთად) |
| წიბოების რაოდენობა | 1 (წრიული კიდე ფუძესთან) |
| წვეროების რაოდენობა | 1 |
| გვერდითი ზედაპირის შლა | წარმოადგენს წრიულ სექტორს |
5. პრაქტიკული ამოცანები (მაგალითები)
აქ მოცემულია ტიპური ამოცანები, რომლებიც დაგეხმარებათ ცოდნის განმტკიცებაში.
მაგალითი 1: მოცულობის პოვნა
ამოცანა: იპოვეთ კონუსის მოცულობა, თუ მისი რადიუსია \(3\) სმ, ხოლო სიმაღლე — \(4\) სმ.
ამოხსნა:
ვიყენებთ ფორმულას: $$V = \frac{1}{3} \pi r^2 h$$
ჩავსვათ რიცხვები: $$V = \frac{1}{3} \times \pi \times (3)^2 \times 4$$
$$V = \frac{1}{3} \times \pi \times 9 \times 4$$
$$V = 3 \times 4 \times \pi = 12\pi \approx 37.68 \text{ სმ}^3$$
მაგალითი 2: სრული ზედაპირის ფართობი
ამოცანა: იპოვეთ კონუსის სრული ზედაპირის ფართობი, თუ რადიუსია \(6\) სმ და მსახველი (\(l\)) არის \(10\) სმ.
ამოხსნა:
ვიყენებთ ფორმულას: $$S_{sruli} = \pi r (l + r)$$
ჩავსვათ რიცხვები: $$S = \pi \times 6 \times (10 + 6)$$
$$S = 6\pi \times 16$$
$$S = 96\pi \approx 301.44 \text{ სმ}^2$$