ცილინდრი (Cylinder)
1. რა არის ცილინდრი?
განმარტება: მათემატიკური განმარტებით, ცილინდრი არის სამგანზომილებიანი სხეული, რომელსაც გააჩნია ორი პარალელური და იდენტური წრიული ფუძე, რომლებიც შეერთებულია მრუდი ზედაპირით.
ძირითადი მახასიათებლები:
- ფუძეები (Bases): 2 წრიული ბრტყელი ზედაპირი (ზედა და ქვედა).
- გვერდითი ზედაპირი (Curved Surface): 1 მრუდი ზედაპირი, რომელიც აერთებს ფუძეებს.
- წიბოები: 2 მრუდი წიბო (სადაც გვერდითი ზედაპირი ეხება ფუძეებს).
- წვეროები: 0 (ცილინდრს კუთხეები/წვეროები არ გააჩნია).
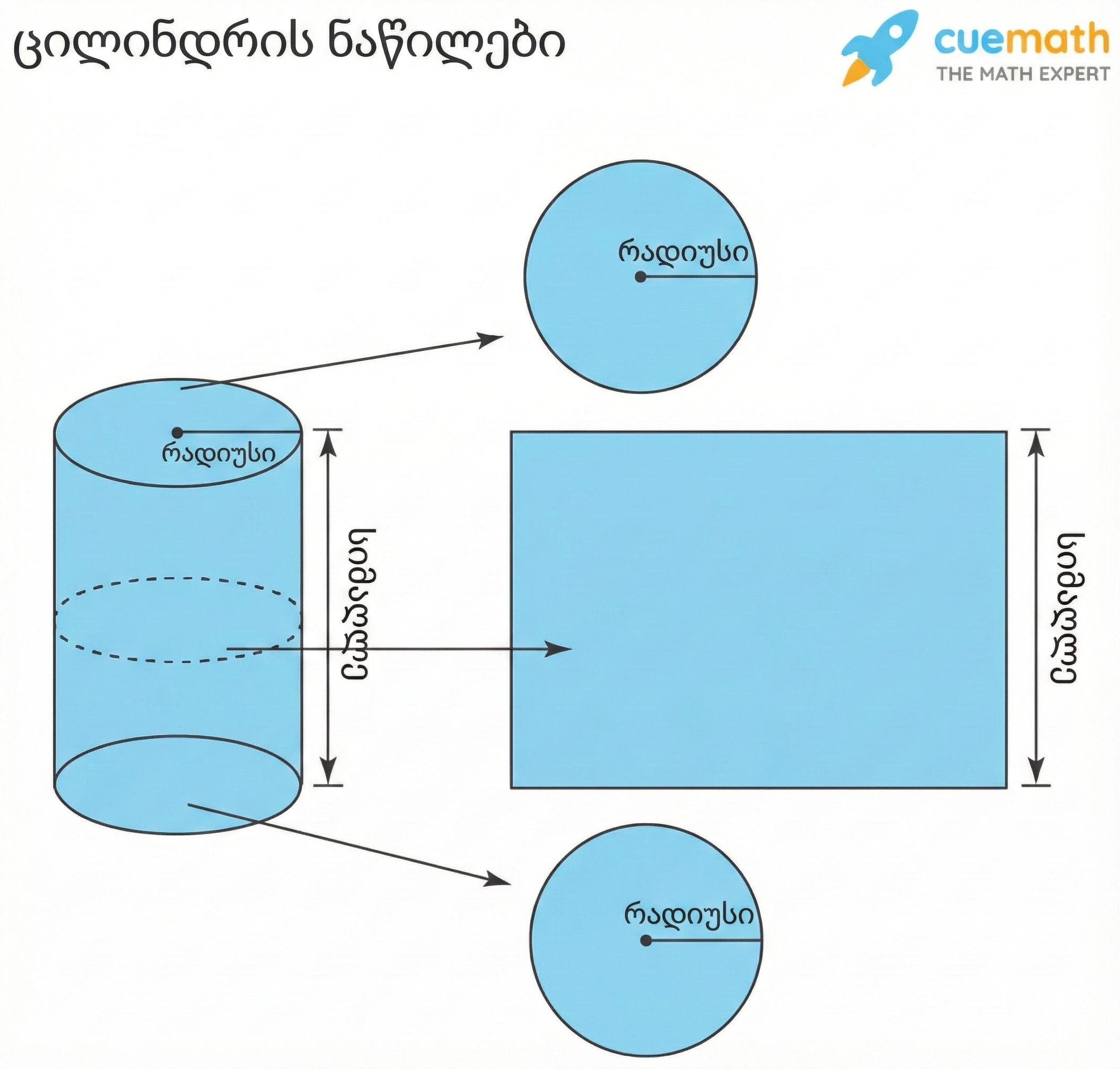
- რადიუსი (\(r\)): მანძილი ფუძის ცენტრიდან მის კიდემდე.
- სიმაღლე (\(h\)): პერპენდიკულარული მანძილი ორ ფუძეს შორის.
2. ცილინდრის ძირითადი ფორმულები
როგორც მათემატიკოსები, ჩვენ ვიყენებთ ზუსტ ფორმულებს სივრცული ფიგურების გასაანალიზებლად. ცილინდრის შემთხვევაში გვაქვს სამი კრიტიკული ფორმულა.
| პარამეტრი | ფორმულა | განმარტება |
|---|---|---|
| გვერდითი ზედაპირის ფართობი (LSA/CSA) | $$2\pi rh$$ | მხოლოდ მრუდი ნაწილის ფართობი (ფუძეების გარეშე). |
| სრული ზედაპირის ფართობი (TSA) | $$2\pi r(h + r)$$ | გვერდით ზედაპირს + ორივე ფუძის ფართობი. |
| მოცულობა (Volume) | $$\pi r^2h$$ | სივრცე, რომელსაც იკავებს ცილინდრი. |
შენიშვნა: ფორმულებში \(\pi\) (პი) არის მუდმივა და დაახლოებით უდრის \(3.14159\)-ს, ან \(\frac{22}{7}\)-ს.
3. ცილინდრების ტიპები
გეომეტრიაში განასხვავებენ ცილინდრის რამდენიმე სახეობას, თუმცა ყველაზე გავრცელებულია ორი მათგანი:
ა. მართი წრიული ცილინდრი (Right Circular Cylinder)
ეს არის სტანდარტული ცილინდრი, სადაც ღერძი (ხაზი, რომელიც აერთებს ფუძეების ცენტრებს) ფუძეების მართობულია. სიმაღლე ზუსტად ემთხვევა ღერძის სიგრძეს.
ბ. დახრილი ცილინდრი (Oblique Cylinder)
ცილინდრი, რომელიც "გადახრილია". აქ ღერძი არ არის ფუძეების მართობული, თუმცა ფუძეები მაინც პარალელურია.
მნიშვნელოვანი: მოცულობის ფორმულა \(V = \pi r^2h\) მუშაობს დახრილი ცილინდრისთვისაც, კავალიერის პრინციპის თანახმად.
გ. ღრუ ცილინდრი (Hollow Cylinder)
წარმოიდგინეთ მილი. ეს არის ცილინდრი, რომელსაც ამოჭრილი აქვს შიდა ნაწილი. მას გააჩნია ორი რადიუსი: გარე რადიუსი (\(R\)) და შიდა რადიუსი (\(r\)).
ღრუ ცილინდრის მოცულობის ფორმულა: $$V = \pi h (R^2 - r^2)$$
4. პრაქტიკული ამოცანები
იმისათვის, რომ მასალა კარგად ავითვისოთ, განვიხილოთ რეალური მაგალითები.
მაგალითი 1: მოცულობის გამოთვლა
პირობა: მოცემულია მართი ცილინდრი, რომლის რადიუსია \(r = 7\) სმ, ხოლო სიმაღლე \(h = 10\) სმ. იპოვეთ მისი მოცულობა.
ამოხსნა:
ვიყენებთ მოცულობის ფორმულას: \(V = \pi r^2 h\)
ჩავსვათ მნიშვნელობები (ავიღოთ \(\pi \approx \frac{22}{7}\)):
\(V = \frac{22}{7} \times 7^2 \times 10\)
\(V = 22 \times 7 \times 10\)
\(V = 1540 \text{ სმ}^3\)
მაგალითი 2: სრული ზედაპირის ფართობი
პირობა: ცილინდრის რადიუსია 3 სმ, სიმაღლე კი 5 სმ. იპოვეთ სრული ზედაპირის ფართობი (TSA).
ამოხსნა:
ფორმულა: \(TSA = 2\pi r(h + r)\)
\(TSA = 2 \times 3.14 \times 3 \times (5 + 3)\)
\(TSA = 18.84 \times 8\)
\(TSA \approx 150.72 \text{ სმ}^2\)
მაგალითი 3: სრული ზედაპირის ფართობის გამოთვლა
პირობა: იპოვეთ ცილინდრის სრული ზედაპირის ფართობი, თუ რადიუსი არის 5 ერთეული, ხოლო სიმაღლე - 6 ერთეული.
ამოხსნა:
ცილინდრის სრული ზედაპირის ფართობი = \(2\pi r(h + r)\)
= \(2 \times 3.14 \times 5 \times (6 + 5)\)
= \(31.4 \times 11\)
= 345.4 კვადრატული ერთეული.
მაგალითი 4: მოცულობის გამოთვლა
პირობა: იპოვეთ ცილინდრის მოცულობა, თუ სიმაღლე = 3 ერთეული და რადიუსი = 7 ერთეული.
ამოხსნა:
როდესაც მოცემულია სიმაღლე და რადიუსი, შეგვიძლია გამოვიყენოთ ცილინდრის მოცულობის ფორმულა.
მოცულობა = \(\pi r^2h\)
= \(3.14 \times 7^2 \times 3\)
= 461.58 კუბური ერთეული.